BACK | CONTENTS | NEXT | OCTONION HOME | MATHEMATICAL IDEAS IN SCIENCE |
Division Algebras, Lie Algebras, Lie Groups and Spinors
Another example
complicates matters a little: let u be as defined above, and let
ρ be a projection operator belonging to
the same algebra. That is, ρ2
= ρ.
Assume ρ commutes with u. (ρ
is an idempotent by definition, but in refering
to it as a projection operator stresses the idea that it acts on some space,
which
will almost always also be an algebra in these pages; also note that not all
spaces
have nontrivial (not equal 1 itself) projection operators - and in fact division
algebras do not, else they would not be division algebras.)
Consider the exponential exp(uρθ):
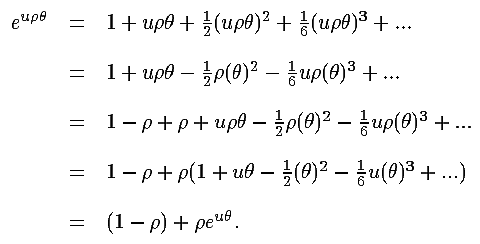
Note that (1 -
ρ)2 = (1 - ρ),
so (1 - ρ) is also a projection operator.
Also,
ρ(1 - ρ)
= ρ - ρρ
= ρ - ρ
= 0. So ρ and (1 - ρ)
are orthogonal projection operators.
In particular, ρ and (1 - ρ)
act on some space: they project subspaces, and these
subspaces must be orthogonal. Because of the equation above it is clear that
the action of exp(uρθ)
on this space is nontrivial only on that subspace projected
by ρ, while the subspace projected by (1 - ρ) is left invariant (a good paradigm
for all this is 2x2 real matrices, with ρ
= diag[1,0]):
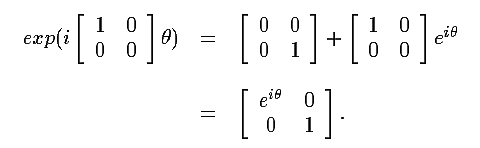
BACK | CONTENTS | NEXT | OCTONION HOME | MATHEMATICAL IDEAS IN SCIENCE |