Division Algebras, Lie Algebras, Lie Groups: 2

Division Algebras, Lie Algebras, Lie Groups and Spinors

2. Exponential Function

One of the most beautiful equations in all of mathematics is the exponential
of a pure imaginary complex number:

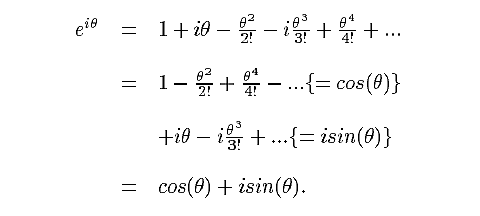
A really big point to make here is the following: the only property of the complex
unit i used by this equation is i² = -1. If u is an element of an algebra that has an
identity (1), and u² = -1, then exp(uθ) = cos(θ) + u sin(θ). We shall use this fact
repeatedly in what follows.

The norm squared (length squared) of the complex number z = x + iy is:
zz* = (x + iy)(x - iy) = x² + y², where z* = (x - iy) is the complex conjugate of z.
The complex conjugate of exp(iθ) is exp(-iθ) = cos (θ) - i sin(θ), so the norm
squared of exp(iθ) is

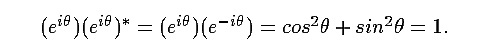
That is, the set of all exp(iθ) is just the unit sphere (circle) in the 2-dimensional
complex plane. This set plays many roles. In particular, it is the 1-sphere, one of
three nontrivial parallelizable spheres (more anon); and it is the Lie group U(1).