Division Algebras, Lie Algebras, Lie Groups: 4

Division Algebras, Lie Algebras, Lie Groups and Spinors

4. U(1) = 1-Sphere: Parallelizable

The set of all unit complexes (norm 1 and can be written in the form exp(iθ)) is closed
under multiplication (exp(ia)exp(ib) = exp(i(a+b)). This set fulfills all the requirements
of a Lie group (roughly: multiplicative closure; inverses; identity; and the full set is a
nice very smooth continuous set (manifold); We needn't go into elaborate rigorous
detail - we'll come to know them when we see them). This Lie group is U(1). The
Lie algebra associated with U(1) is the set from which U(1) is derived via exponentiation:
hence the Lie algebra of U(1), which we denote u(1), is the set {iθ: θ real} - the set
of purely imaginary complex numbers.

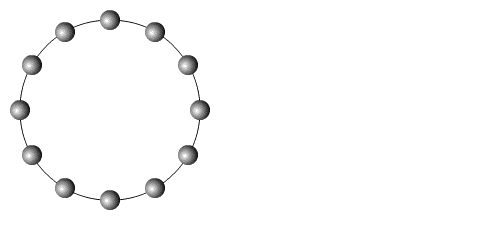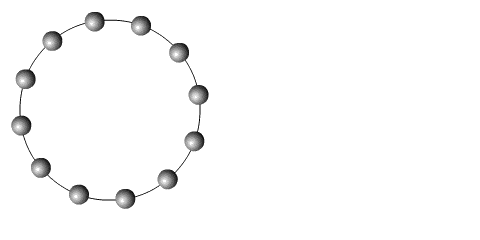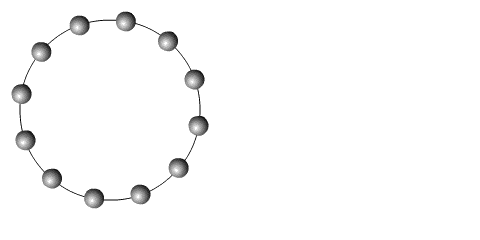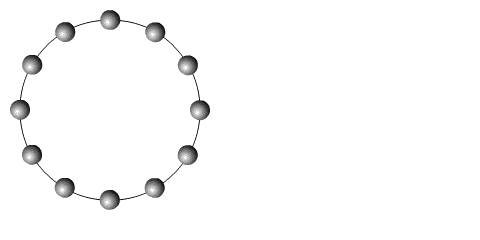
The associated manifold is the circle, the 1-dimensional sphere. This manifold
has a special property: it's parallelizable (all Lie groups are, but only three spheres -
although two of these three parallelizable spheres are also Lie groups - more anon).
This can be visualized as follows: a manifold is parallelizable if it is possible to set
all its points in smooth flowing motion at the same time (a good example of a
nonparallelizable manifold is the 2-sphere (surface of a ball). There is always at least
one point on the surface of a ball that is stationary: it's impossible to set them all in
smooth motion at once (the fact that the earth has poles is related to this)). It must
be further specified that at any point of the manifold the smooth flowing motion can
flow in any direction. Clearly this is an area where mathematical rigor would be of some
use, but our intention here is simply to introduce the concept as a way of highlighting
the exceptional nature of the 1-, 3- and 7-spheres.

Spin a 1-sphere and all the points move at once (not so a 2-sphere). It's clearly
parallelizable.

There are two ways to view this parallelizablility: the 1-sphere is also the Lie group U(1),
and all Lie groups are parallelizable; and the 1-sphere is the set of all unit complex
numbers, and the complex numbers are a division algebra - and it can be shown that the set
of all unit elements of any such division algebra must be parallelizable. There are
three hypercomplex division algebras; and there are three nontrivial parallelizable
unit spheres - three spheres on which all points may move at once.