Division Algebras, Lie Algebras, Lie Groups: 1

Division Algebras, Lie Algebras, Lie Groups and Spinors

1. Exponential Function

Some familiarity with algebraic concepts is assumed, but as this material will stress
utility over rigor, there will be no theorems, axioms, corollaries or lemmas. So, when
we say that A and B are elements of an algebra, we understand that they can be
added (A + B), subtracted (A - B), and multiplied (AB), and in all cases the result is
an element of the same set we started with. And if x is a real number, then xA is
also an element of that set. Any generalizations of these ideas will occur as needed.

Let R be the algebra of real numbers, and C be the algebra of complex numbers.
C is 2-dimensional over the reals: each complex number z = x + iy has a real part
and imaginary part (x and y are real numbers, so x is the real part of z, and iy the
imaginary part).

In Lie group theory the exponential function is extremely important. The exponential
of a real number is something one can easily determine by punching the number into
a calculator and hitting the "e^x" button. The answer is a positive real number. But
a calculator figures out this answer by expanding the exponential function in a
Taylor series - and infinite polynomial sum (the calculator uses enough of the terms
of the infinite sum to be as accurate as its screen allows). The Taylor expansion of
exp(A) = e^A is given below:

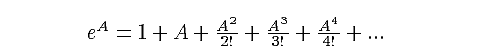
If A is a real number, then the answer is a real number. But the righthand side of
this equation can be defined for many other kinds of algebraic objects. This
expression can be defined for any of the kinds of algebras we will deal with here.
It uses algebraic addition, multiplication, and the multiplication by scalars (real
numbers). Mathematicians worry about it being "well-defined", meaning that there
is some unique algebraic answer to the infinite sum. We'll let them worry about
that: all of our exponentials will be well-defined.