Division Algebras, Lie Algebras, Lie Groups: 6

Division Algebras, Lie Algebras, Lie Groups and Spinors

6. Quaternions: Introduction

Let q_j, j = 1,2,3, represent the pure imaginary quaternion units (let q₀ = 1). The multiplication
table of the pure quaternion units is cyclic (see above). Add to this the fact that these units
anticommute and you've got the whole multiplication table. It's interesting to represent
these units by matrices, and our first representation will be by real 4x4 matrices. For example:

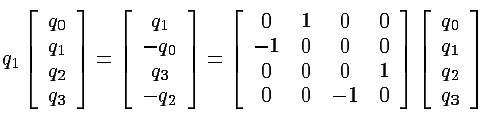
Note: because the Q imaginary units anticommute, multiplication by this same element from
the right will yield a different matrix (the lower right block is the negative of that given above).
So, we have the identity from q₀ (left or right multiplication), three matrices by left
multiplication of imaginary units, and three by right multiplication. And then there are 9 = 3x3
from simultaneous left/right multiplication by imaginary units (indices = 1,2,3). That makes
1+3+3+9 = 16 in all, and in fact these 16 matrices form a basis for the 16-dimensional
real algebra of 4x4 real matrices (R(4)).

If you bother to compute the 3 left multiplication matrices, and 3 right multiplication matrices,
you should find that the left (or right) multiplication matrices anticommute with one another,
but each of the left multiplication matrices commutes with each of the right multiplication
matrices. The adjoint algebra of left actions of Q on itself commutes with the adjoint algebra
of right actions (as we will see, this is related to the following Lie algebra identity:
so(4) = su(2) x su(2); ie., the 6-dimensional Lie algebra so(4) consists of two commuting
copies of the 3-dimensional su(2)).